Derivatives-Options

Types of option

Long (+)	Put (-)
Enjoys the rights	Suffers on obligation
Pays initial premium	Receive initial premium
Pays of will be positive or zero	Pays of may be negative or zero
Suffer time decay	Enjoys time decay
Long on volatility i.e. gains if volatility rises	Short on volatility i.e. gains if volatility

Based on maturity

American	European
Can be exercised on or prior to maturity. Eg stock option in India	Can be exercised only on maturity. Eg Index option in India

Based on right

Call	Put
Right to buy	Right to sell
Bullish	bearish
Pay off : Max (s-E/0)	Pay off : Max (E-S/0)
1.Intrinsic value = Max (S-E,0)	1.Intrinsic value = Max (E-s,0)

 

Moneyless of an option

Option	S<E	S=E	S>E
Call	Out of the money	At the money	In the money
Put	In the money	At the money	Out of the money

 

Intrinsic value	Time value
F(S,E)	F(t,δ,r), f (time,volatility, risk free rate of int)
C+ is a substitute of S+, Since C results in saving interest, call is a positive function of interest rate.	Time: higher the time left to maturity, more valuable is the option
P is substitute of S-,since P+ results in loss of interest . Put is a negative function of interest rate	Volatility: If volatility causes the option to be exercised , higher volatility benefits the option buyer , however if volatility causes the option to lapse, pay off is zero, higher the volatility higher the option value

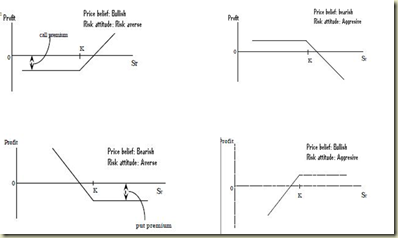
Pay off profile & profit diagram of an option

Hedging through options

Hedging foreign currency payable (C+,P- relationship)

Alt I: Buy calls (C+)

Alt II: Sell a put (P-)

Alt III: Buy calls (C+), Sell a put (P-) at the same E

Alt IV: P- at a lower E(E1) & C+ at a higher E(E2) such that net premium is NIL.

Hedging foreign currency receivable (P+,C- relationship)

Alt I: Buy Put (P+)

Alt II: Sell a call (C-)

Alt III: Buy puts (P+), Sell a call (C-) at the same E

Alt IV: Range forwards (P+ at E(E1) & C+- at a E(E2) [E1<E2]

Speculation using options

A) Synthetic strategies

Strategy I: Protective put ( P+;S+)

This involves buying a stock & hedging the downside by buying a put. Its profit profile would be similar to long call (C+)

Therefore P+, S+=C+

Strategy II: Covered call writing ( P+;S+)

This involves buying a stock (S+) & for going the upside of the stock by writing a call (C-) which in turn reduces the effective cost of holding the share.

We will find that this strategy is equivalent to put writing i.e. S+;C-= P-

B) Combination strategies

C) Spread strategies

i.Time/calendar horizontal spread: Same strike price but different maturity

ii.Price/vertical spread: Same maturity but different strike price

• Butterfly spread: based on volatile/non-volatile price belief, It will involve 3 strike price ( C+,2C-,C+)
• Bull & bear spread : It will involve two strike price

iii.Diagonal spread: Different maturity and different ‘E’

 

 

Valuation of option

The value of an option i.e. option premium comprises of

A. intrinsic value

B. Time value

This functional relationship need to be opened out in the form of option pricing model

A Binomial model

B. Black scholes

Before we evaluate this model let us cover put- call parity.

Put- call parity

It is a relationship between European put and call option on the same stock for the same maturity at the same E. It is given by

Po + So = Co + PV of E

This parity is based on prevention of arbitrage principle. If two portfolios have identical pay off the cost of portfolios should be same to prevent arbitrage.

BINOMIAL MODEL

Option pricing requires the specifications of the stock price behavior. The binomial model is based on a simple assumption that if stock price today is S it can take up only two value uS and dS on maturity .

The pricing of options via binomial model can be done by two methods

Method 1- Risk free portfolio approach

Method 2- Risk neutralization Approach.

Black scholes model (BSM)

BSM is a limiting case of binomial model. As the nos of steps om the nomp,oa; ,psde; tends to infinity the binomial model tends to BSM

BSM is an elegant model & elegancy has been obviously achieved by taking a no. of assumptions

1.Markets are efficient ( i.e. no transaction cost , no taxes, no restrictions on short selling & perfectly divisible securities)

2.Options are only European

3.Option are on non-dividend paying stocks

4.Risk free continuously compounded interest rate (ir) is known & constant

5.The Annualised volatility of stock return is know as constant

6.Stock price are log normally distributed

 

Option Greeks

We know that option price = f(S,E,r,t,δ)

Thus option pricing continuously change in the mkt on account of change in these factors. The sensitivity of option price with each factor, taking others constant is know as option Greeks.

Delta

It is sensitivity of option premium to stock price

Delta of a call is potive & that of put is negative. Thus if delta of call is 0.4, it means that if share price goes up by re1, call predecessor relation is expected to rise by 0.4

Theta

It is the rate at which time decay occur, at par

Theta is negative for both call & put. Thus if theta of call is -4, it means that with the passage of a day call premium is expected to fall by Rs4/-

Vega

It is sensitivity of option premium to volatility at par

Vega is positive of equal for both call & put. Thus if Vega of an option is 7, it means that if volatility goes up by 1%, option prem is expected to rise by Rs7.

RHO

It is sensitivity of position premium with int. rate, at par

Rho of a call is positive & that of a put is negative. Thus if rho of a call is 0.7, it means that if int. rate goes up by 1%, call prem is exp to rise by Rs 0.7.

Gamma

It is the rate of change of delta wrt stock price, at pat

Gamma is positive & equal for both call & put. Thus if gamma of a option is 0.03 it means that if share price goes up by Re1, delta of the option is expected to rise by Rs0.03.

Derivatives-Futures

Definition:

Futures are standardized forward contracts traded on an exchange with marked to market features and strangened margin requirement. Futures are considered to be a leveraging tools i.e. instead of buying the stock a trader can buy futures by putting only a fraction of the share price as margin.

Margin requirement

Initial margin, maintenance & variation

Futures vs forwards

Both futures and forwards refer to contractual obligation to buy or to sell an asset at some future date at a pre determined price. However since forwards are OTC & futures are exchange traded there are some differences

Since futures involve cash inflows & outflows in between there is a time value of money factor which is absent in case of forwards whether future price is absent in the case of forwards whether future price should be higher or lower, then its equivalent forward price is summarized in the chart below.

Open interest

It is the number of future contract that has not yet been squared off. Those who trade in future can take up the following positions

A fresh long & a fresh short position leads to a higher open interest. A fresh long/short combined with a squaring off short/long transaction leaves open interest unchanged finally a squaring off long & squaring off short position leads to decrease in open interest.

As a new future contracts open , fresh position are taken up resulting in higher open interest. However as we approach maturity traders starts squaring up their position such that open interest falls. On the maturity date all outstanding contracts are deemed to have been squared off. i.e. open interest=Zero

Days	A	B	C	D	Open Interest
1	5	12	7		12
2	20	12	10	42	42
3	15		5	12	22
4	10		12	22	0

Traders look at the future price movement together with a change in open interest to judge direction of the price. A change in future price if complement with a higher open interest supports the direction of the change & vice versa.

Therefore

Rise in F & increase in open interest : Bullish; Rise in F & decrease in open interest : Neutral

Fall in F & increase in open interest : Bearish; Rise in F & increase in open interest : Neutral

Relationship between Spot price & future price:

As per the cost of carry model

Future price: Spot price + net cost of carry

Where net cost of carry:

Interest saved + storage cost saved-monetary benefit forgone –convenience yield foregone if net cost of carry is positive/negative, we have future price higher/lower then spot price and the market is set to be in Contango/backwardation. We also define the term called bases, which is the difference between spot price and future price i.e. bases=spot-future. Bases is negative/positive under Contango/backwardation. As we approach maturity bases narrows down to zero.

Mathematisation of the cost of carry model

The cost of carry model when applied to stock, future will capture only the interest and dividend component. The exact procedure of computing future depend s upon nature of information given

Case 1- interest rate is not effective and dividend yield is given.

Case 2 – if interest rates and dividend yield are annualized effectives

Case 3 – if interest rate and dividend yield are continuously compounded

Stock future arbitrage

If the cost of carry model doesn't hold good there should be an arbitrage opportunity

Case I – cash and carry arbitrage.- If actual futures >theoretical futures, futures are relatively overpriced and spot is relatively under-priced.. so we carry out cash and carry arbitrage i.e buy spot and sell future.

Case II – reverse cash and carry arbitrage.- If actual futures < theoretical futures, futures are relatively under priced and spot is relatively over priced.. so we carry out reverse cash and carry arbitrage i.e buy futures and shot sell the stock.

Irrespective of the type of arbitrage, arbitrage profit will be equal to the amount of mis-pricing i.e difference between actual future and theoretical future

Stock index futures

These are futures on a well published benchmark index such as Nifty, Sensex, bank Nifty etc. since the underline is a hypothetical stock index futures are compulsorily cash settled i.e. non deliverable.

Stock index future can be used to speculate on the overall market or a particular sector. Thus if a trader is bullish on banking stock in general he may go long in bank nifty futures say at Rs 1250 with a multiple or lot size of 250 say. If his bullish options turn out to be correct he may able to square of at a higher price Rs 1310 say making a profit of (1310-1250)x 250=Rs 15000

Stock Index Arbitrage

This is normal cash and carry or reverse cash and carry arbitrage.

Limitation of Stock Index Future

1. Margin requirement
2. Transaction cost
3. Dividend risk
4. Taxes
5. Implementation delays and lack of liquidity
6. Tracking error i.e. difference in composition of actual index in the portfolio constructed by the arbitrager

Beta management using Stock index futures

Fund managers may bring about a change in beta of their portfolio by using stock index futures. If they want to increase/decrease they need to buy/sell stock index future.. The no of futures contract to be purchased is given

βT=   Target beta (if not given taken as 0)

βP=   Existing Beta of the portfolio

βF=  Beta Future (not give take as 1)

Currency Futures

a) Pricing and Arbitrage- Currency futures are priced as per IRP.

If IRP dose not hold good there will be an opportunity for covered interest arbitrage.

b) Hedging through currency futures

If a firm has foreign currency payable it is obviously afraid of foreign currency appreciating against its home currency . to hedge the same it should buy future on foreign currency since futures are standerdised it may have to underhedged or overhedged.

On the maturity date of the payable , futures are squared of resulting in a profit /loss. The payable is met by way of spot purchase . We accordingly compute the overall HC outflow.

Similarly foreign currency receivable is hedged by selling future on foreign currency. On the date of receivable futures would be squared off and the receivable will be sold spot. We hence compute HC inflow on maturity.

Future cover is a imperfect hedge as it reduces the uncertainty rgarding the FC outflow /inflow in settling the FC payable /receivable but dose not eliminate.

There are two reasons for imperfection

• Standardization (amount and maturity mismatch)

• Bases risk (spot and future do not move at the same rate).

Speculation using currency futures

Derivatives- Basic

Definitions

Derivatives may be defined as any financial contract or instrument which derives its value from underlying. The underlying can be stock , index, currency commodity , temperature, rainfall & what not.

Types of derivatives

Forward commitments & contingent contract

Types of derivatives

Over the counter	Exchange traded
Customized features
No margin requirement\
Less regulated
Counter party can default
Lower liquidity
Generally suitable for hedging

Participants of derivatives

Hedges: They already have an exposure & take a derivative position to offset the exposure

Speculators: They have a price belief & a risk tolerance level. They create a position in the derivative market to make profit from their price belief knowing fully well they can lose

Arbitrageurs: They spot mis-pricing & take long short position with a view to make riskless profits

Pricing of derivatives:

Derivatives are priced on the prevention of arbitrage principle i.e. the price of derivative should be such that no body carry out arbitrage

Financial Swaps

The financial swaps may be defined as a exchange of a stream of cash flow. A financial swap is over the counter (OTC) products & therefore comes in various flavors.

a) Plain vanilla Interest rate swaps:

It is a fixed floating interest rate swaps with a notional principal & netting features

Consider the terms of a financial swap

Notional principal: $100000, maturity 5 years, floating rate LIBOR, fixed rate 10%, and periodicity: annual. A is fixed rate payer & B is the fixed rate receivers

Suppose LIBOR at the beginning of each year over the 5 yeas period turnout to be 11%,13%,9%,8% & 12%.

b) Currency swap

In this case the payments are swapped into two different currencies without netting features. The principal amounts are not notional. There is an actual exchange of principal at the beginning & exchanged at the end of swap

Suppose A & B enters into a currency swap of maturity 5 years in which A receives 10% of ℓ100000 fixed and B pays 10% on $200000 every year (at the initiation of Swap ℓ1=$2)

Step 1: exchange of principal at T=0

Step 2: Annual interest transfer without netting

Step 3: Re exchange of principal at t=5

c) Equity swap:

This involves swapping equity return vs some fixed & floating interest based on notional principal with netting features

D) SWAP quotations

Banks act as market makers and provide bid-ask rate in the swap market. These rates are the fixed quotes vs a floating rate say LIBOR. The fixed quotes are generally expressed as a spread over treasuries.

Thus if a bank quotes 5 yrs fixed to floating swap at 60/90 basis points over treasuries vs LIBOR & 5 yrs treasuries are yielding 7.5%.

The quotes implies that

Bank is willing to pay (7.5+0.6) i.e. 8.1% fixed & receive LIBOR

Bank is willing to receive (7.5+0.9) i.e. 8.4% fixed & pay LIBOR

Thus if the bank is luckily stuck equally on both sides of the quote it looks in a spread of 0.3% as shown below.

E) SWAP based on a comparative advantage

Merger & acquisition

M&A is an inorganic growth strategy as compared to organic growth, M&A is a shortcut. However this shortcut is at same time costly. The acquirer justifies that the premium paid on grounds of SYNERGY

Synergy is the potential additional value resulting from M&A. It has been most used & misused rational for merger.

Source of Synergy:

1. Economics of scale
2. Avoidance of competition
3. Creation of monopoly power
4. Utilization of surplus fund complimentary resources
5. Tax shield
6. Improvement of marginal efficiency

Dubious reasons for merger

Diversification benefit: Shareholder can diversify at portfolio level

Boot strap effect: a high PE company acquiring a lower PE co resulting in higher post merger EPS which is just an illusion as post merger PE ratio should fall.

Type of mergers

1. Horizontal : Same business, same stage
2. Vertical: same business, different stage
3. Conglomerate: different & unrelated business (Risky)

Financial evaluation of merger proposal

Case I: Cash deal

VAB=VA + VB + synergy-cash

NPVA=VAB-VA

NPVB=cash-VB

NPVA + NPVB=Synergy

Case II: Stock deal

Exchange ratio (r) is the no. of share of A i.e. issued for every share of B. It may be fixed as follows:

Based on EPS: r = EPSA/EPSB

Based on Book value: r=BV of per share of B/BV per share of A

Based on MPS: r = PB/PA

Based on Intrinsic value: r= Intrinsic value B /IVA

XYZ Ltd., is considering merger with ABC Ltd. XYZ Ltd.’s shares are currently traded at Rs. 20. It has 2,50,000 shares outstanding and its earnings after taxes (EAT) amount to Rs. 5,00,000. ABC Ltd., has 1,25,000 shares outstanding; its current market price is Rs. 10 and its EAT are Rs. 1,25,000. The merger will be effected by means of a stock swap (exchange). ABC Ltd., has agreed to a plan under which XYZ Ltd., will offer the current market value of ABC Ltd.’s shares:

(i) What is the pre-merger earnings per share (EPS) and P/E ratios of both the companies?

(ii) If ABC Ltd.’s P/E ratio is 6.4, what is its current market price? What is the exchange ratio? What will XYZ Ltd.’s post-merger EPS be?

(iii) What should be the exchange ratio, if XYZ Ltd.’s pre-merger and post-merger EPS are to be the same? (10 marks)(May 2003)

The following information is provided related to the acquiring Firm Mark Limited and the target Firm Mask Limited:

	Firm Mark Ltd	Firm Mask Ltd
Earning after tax (Rs.)	2,000 lakhs	400 lakhs
Number of shares o/s	200 lakhs	100 lakhs
P/E ratio (times)	10	5

Required:

(i) What is the Swap Ratio based on current market prices?

(ii) What is the EPS of Mark Limited after acquisition?

(iii) What is the expected market price per share of Mark Limited after acquisition, assuming P/E ratio of Mark Limited remains unchanged?

(iv) Determine the market value of the merged firm.

(v) Calculate gain/loss for shareholders of the two independent companies after acquisition

Foreign Exchange: Exchange change determination

The basic theories underlying the exchange rates –

1. Law of One Price: In competitive markets free of transportation costs barriers to trade, identical products sold in different countries must sell at the same price when the prices are expressed in terms of their same currency.

Purchasing power parity: As inflation forces prices higher in one country but not another country, the exchange rate will change to reflect the change in relative purchasing power of the two currencies.

2. Interest rate effects: If capital is allowed to flow freely, the exchange rates stabilize at a point where equality of interest is established.

Interest rate Parity

Meaning of IRP-It is a relationship between exchange rates and interest rates other factors remaining constant. As per IRP if interest rate in country A are higher than that in country B the currency of country B should be at a forward premium. Thus if interest rate is 12% in India while interest rate is 5 % in Us dollar should be at a forward premium against Re.

IRP goes on to quantify the forward premium to be equal to the interest rate differential in the approx terms . Thus dollar should be at a forward premium against Re approximately by 12-5=7% and exactly by 7/1.05= 6.67 %.similarly Re should be at a forward discount against dollar approximately by 7% and exactly by 7/1.12 = 6.25 % . I formal terms the IRP equation may be given by

Adding 1 to both sides we have

The ratio of forward to spot rates should be equal to the ratio of interest rate factors. Since forward contracts are available for short term maturities say 1m , 3m, 6m at a periodic adjustment is required . So we have

Rational for IRP

IRP must hold good to prevent covered interest arbitrage .

Cover interest arbitrage involves

i.Borrow one currency (say currency A) and compute currency A outflow on Maturity.

ii.Use the borrowed amount of currency A to buy currency B spot.

iii.Invest currency B and compute currency B receivable on maturity.

iv.Sell currency B receivable forward to get back currency A.

If inflow of currency A from step 4 is greater than the outflow from step 1 there has been a covered interest arbitrage opportunities.

Application of IRP

Forward cover versus money market cover

We had earlier discussed forward cover for the purpose of hedging payable/receivable. However the forward rate might be under priced/over priced. Hence we introduce a new cover called money market cover.

Foreign currency payable

1. Invest the PV of the FC payable.

2. Buy the investment amount spot

3. Borrow home currency and compute FC outflow on maturity.

Foreign Currency receivable

1. Borrow the PV

2. Sell the borrowed amount spot.

3. Invest home currency and compute the HC inflow on maturity.

Purchasing power parity

PPP is a relationship between exchange rate and inflation other factors remaining constant. Inflation erodes the purchasing power of money so a country with higher inflation against another should experience a depreciation of its currency. There are three forms of PPP

1. Absolute form
2. Relative form
3. Expectations form .

Absolute form Of PPP

This is based on law of one price and prevention of commodity arbitrage. Consider a common basket of commodity which sell in India for Rs 900 and in US $ 20. We have $ 20 = Rs 900 or 1 $ =Rs 45. so as per absolute PPP the exchange rate between two currencies should be equal to ratio of the price of common basket of commodities. Now suppose it happens 10% inflation in India and 4 % in UK.

Relative form Of PPP

The relative form relates the past in exchange rate with the levels of inflation to find out the real appreciation depreciation of the currency.

Suppose in the Re & $ example under absolute PPP, $ appreciates only by 2% ( Say) against Re compared to 5.77%. Therefore $ has depreciated in real terms, If $ appreciates by 5.77% exactly there is no real appreciation or depreciation of $. Finally if $ appreciates by 7% ( say), there has been a real appreciate of $.

If Re falls by more/less/equal to 5.45% we say Re has depreciated/appreciated/remain unchanged in real terms

The concept of real appreciation/depreciation is relevant in

a)Determining the competitiveness of a country & export i.e a country’s export will become more competitive, if its H.C depreciates in real terms

b)Determining the real return earned by domestic vs foreign investor

To compute mathematically the real appreciation/depreciation of a currency, let us the following numbers

Spot rate 1year ago (So)= Rs46/$

Spot rate is right now (S1)= Rs51/$

Inflation in india & US last year happened to be 7% & 3% respectively.

Find nominal & real appreciation or depreciation of each currency

Expectation form Of PPP

The expectation form of PP is used to forecast long term exchange rates based on predicted levels of inflation. There could be deviations from PPP in the form of real appreciation or depreciation. Thus if spot rate right now is Rs50/$ & inflation forecast for the next year for India & US are 7% & 3%.

S1 = 50*(1.07)/(1.03) = Rs 51.94

However if Re is expected to appreciate by 1% in real terms: 51.94/1.01 = 51.43

In finding out the cost of ECB, a long term forecast as per PPP is often made.

International Fisher effect (IFE)

Assume that exchange rates will change in direct proportion to relative differences in long term interest rates.

Assumes that long term interest rates capture the market’s expectation for inflation.

Countries with relatively high rates of long term interest rates (i.e., high inflation) will show currency depreciation.

Countries with relatively low rates of long term interest rates (i.e., low inflation) will show currency appreciation.

In equilibrium, the amount of depreciation (or appreciation) will be equal to the long term interest rate differential.

Foreign Exchange: Risk management

TYPE OF FOREIGN EXCHANGE EXPOSURE

A) Transaction exposure

It relates to a firm having a known foreign currency payable/receivable, the home currency equivalent of which is not known with certainty.

B) Operating/economic exposure:

This exposure is an indirect exposure faced by all firms

Case I: Indian firm exporting to US but invoicing in Rupee

Case II: A purely domestic Indian firm ( no export/import) selling goods in India & facing import competition.

Case III: A purely domestic Indian firm ( no export/import) no foreign competition is also affected by exchange rate changes due to interlinked between exchange rate & other macro variables

C) Accounting/Translation exposure

It deals with translation of financial statement of foreign subsidiaries & branches into the parent company home currency. Since no cash flow are involved, it should be notional, however, if markets are inefficient it may effect the share price & is therefore relevant.

TECHNIQUES OF HEDGING TRANSACTION EXPOSURE

Internal	External
Leading & lagging	Forward cover
Invoicing	Money market cover
Outsourcing	Futures cover
Netting	Options cover

Leading & lagging

The maturity of payable or receivable can be pre-pond or post-pond depending on the strength or weakness of the currency normally it is advisable to:

1. Lead the payable in a strong currency
2. Lag the payable in a weak currency
3. Lag the receivable in a strong currency
4. Lead the receivable in a weak currency

Invoicing

Invoicing as a hedging techniques means that an Indian exporter/importer should have the invoice drawn in rupee. Although this will remove transaction exposure it would create economic exposure

Normally invoicing is done in the seller’s currency unless the bargaining power of the buyer is high There can also be the case of dual; invoicing or third currency invoicing

Given a choice regarding the currency of invoicing an Indian exporter should choose that currency which will result in maximum rupee inflow.

Outsourcing

Outsourcing involves importing raw materials from the country to which the firm is exporting. Thus if an Indian firm exports to US, it has $ receivable ( transaction exposure). The firm may create a natural hedge by importing from US. IF it is not possible to import from US, the firm may import from some other country, where currency is significantly positively correlated to $. This is known as the cross hedge.

Netting

This involves netting of the receivable & payable in order to save transaction cost. If there is a maturity mismatched. One can use leading & lagging along with netting to save transaction cost.

Forward contract:

An importer / Exporter has a foreign currency payable/ receivable and is therefore afraid of foreign currency appreciating / Depreciating. To hedge the payable /receivable the importer/ exporter should buy/sell the foreign currency forward. Once the forward contract is entered it is a perfect hedge and the spot rate later on is irrelevant. The decision to go for forward cover or remain unhedged should depend upon a comparison between the forward rates and expected spot rates. If F is favorable the firm should definitely go for forward cover. However if E(S) is favorable the firm may remain unhedged only if its risk tolerance level allows it to take the currency risk.

A company operating in a country having the dollar as its unit of currency has today invoiced sales to an Indian company, the payment being due three months from the date of invoice. The invoice amount is $ 13,750 and at todays spot rate of $ 0.0275 per Re. 1, is equivalent to Rs. 5,00,000.

It is anticipated that the exchange rate will decline by 5% over the three months period and in order to protect the dollar proceeds, the importer proposes to take appropriate action through foreign exchange market.

The three month forward rate is quoted as $ 0.0273 per Re. 1.

You are required to calculate the expected loss and to show, how it can be hedged by forward contract (May 1998).

Money market operation:

In a money market operations, the exposed position in a foreign currency is covered through borrowings or lending in the money market. Money market involves:

Borrowing in FC and invest in HC, in the3 case when FC is to be received in future/export/receivable

Borrowing in HC and invest in FC in the case when FC is to be paid in future/imports/payables

Currency swap:

In a currency swap two parties agree to pay each others debt obligation denominated in different currencies.

A currency swap involves:

An exchange of principal amount today

An exchange of interest payments during the currency of loan

A re-exchange of principal amounts at the time of maturity

Option Forward Contract

This is special type of forward contract in which the customer enjoys the option to buy/sell the foreign currency at any time within a certain future period. The bank therefore quotes either the beginning of the option period or end of option period forward rate which is unfavorable to the customer.

Airlines Company entered into an agreement with Airbus for buying latest plans for a total value of F.F. (French Francs) 1,000 Million payable after 6 months. The current spot exchange rate is INR (Indian Rupees) 6.60/FF. The Airlines Company can not predict the exchange rate in the future. Can the Airlines Company hedge its Foreign Exchange risk? Explain by examples. (November, 2001)

Foreign Exchange-Basics

Foreign Exchange Market

It is an over the counter market where currencies are bought and sold against one another. RBI regulates the markets and appointed banks who act as authorized dealers. Banks acts as market makers and provide bid- ask rates.

Purchase and sale of foreign currency

Nostro Account:

Vostro Account:

Retail Market

The forex market can be divided into three tiers

1. transaction between RBI and authorized dealers

2. Inter-bank or wholesale market.

3. Retain market.

The rate applicable in the retail market are known as telegraphic transfers or TT rates. These rates are arrived by charging TT commission to the inter-bank rate.

Exchange rate quotation

Direct quote:

Indirect quote:

American quote vs merchant quote :

Inter-bank quote vs merchant quote :

Inverse quote :

Cross Rates :

Bid Ask Spread

Depends upon:

1. Turnover of the currency. Higher the turnover, lower the bid-ask spread & vice versa
2. Competition between the market makers. Higher the competition exists, lower the spread & vice versa

Spot and forward rates

Spot rates is a rate applicable for a spot transition i.e. delivery 2 business days ahead. Forward rate is the rate applicable in a forward contract i.e. a contract to buy or to sell foreign currency at a some future date at a rate agreed upon today. Both spot and forward rates are determined by demand and supply forces. Thus forward rates can be higher/lower then spot rate and accordingly the currency is said to at a forward premium or discount

Annulated forward premium or discount

Annualised forward premium on currency B:

A negative discount will imply a discount

Swap Points

Swap points refers to difference between the spot and forward rate. The swap points are low/ high, they are added to the spot rate. Similarly the swap points are high/ low, they are deducted from the spot rates.

Exchange margin

Exchange margin is the extra amount or percentage by the bank over and above the rate quoted by the bank it represents commission, transaction related expenses etc

Arbitrage

Arbitrage refers to simultaneously buying and selling identical/Similar assets with a view to make risk-less profit. Two way arbitrage in a currency market involves buying one currency from a bank and selling it to another bank to make a profit.

• Geographical arbitrage:
  • Two way arbitrage
  • Inverse rates and two way arbitrage
  • Three way arbitrage
  • Cross Rates
• Covered interest arbitrage

Followings are the spot exchange rates quoted at three different forex markets :

USD/INR 48.30 in Mumbai

GBP/INR 77.52 in London

GBP/USD 1.6231 in New York

The arbitrageur has USD1,00,00,000. Assuming that there are no transaction costs, explain whether there is any arbitrage gain possible from the quoted spot exchange rates. (Nov. 2008)